Що таке лінза?

 Лінза (сферична) — прозоре тіло, обмежене з двох боків сферичними поверхнями*.

За формою лінзи поділяють на опуклі й увігнуті .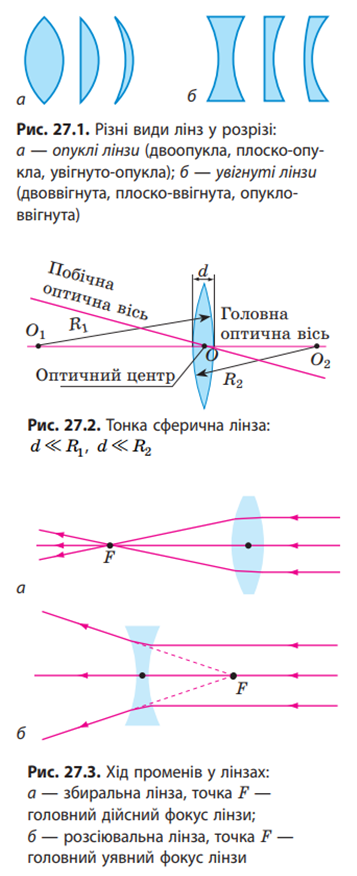

Якщо товщина d лінзи у багато разів менша, ніж радіуси R1 і R2 сферичних поверхонь, що обмежують лінзу, то таку лінзу називають тонкою . Далі йтиметься саме про тонку лінзу.

Пряму, яка проходить через центри сферичних поверхонь, що обмежують лінзу, називають головною оптичною віссю лінзи. Точку лінзи, яка розташована на головній оптичній осі і через яку промені світла проходять не змінюючи свого напрямку, називають оптичним центром лінзи.

Дія лінзи ґрунтується на явищі заломлення світла: світловий промінь, який падає на лінзу, заломлюється на одній із її сферичних поверхонь, поширюється прямолінійно всередині лінзи і знову заломлюється на другій поверхні лінзи .

Якщо промені, що падають на лінзу, виходять із однієї точки, то після проходження через лінзу вони теж збираються (перетинаються) в одній точці, тобто лінза дає зображення точки, а отже, і предмета як сукупності точок.

Однією з головних властивостей лінзи є те, що паралельні промені після заломлення в лінзі перетинаються в одній точці або в одній точці перетинаються продовження заломлених променів. Якщо паралельні промені, пройшовши крізь лінзу, збираються в одній точці, то така лінза є збиральною . Якщо паралельні промені після проходження крізь лінзу йдуть розбіжним пучком, а в одній точці перетинаються продовження цих променів, то така лінза є розсіювальною .

Точку F, у  якій після заломлення збираються промені (або їх продовження), які падають на лінзу паралельно її головній оптичній осі, називають головним фокусом лінзи.

Головний фокус збиральної лінзи є дійсним (у точці F перетинаються власне заломлені промені), а розсіювальної лінзи — уявним (у точці F перетинаються продовження заломлених променів). Кожна лінза має два головні фокуси, розташовані на однаковій відстані від оптичного центра лінзи.

У разі коли паралельні промені падають на лінзу не паралельно її головній оптичній осі, точку, в якій перетинаються ці промені (або їх продовження) після заломлення в лінзі, називають побічним фокусом лінзи (точка F1 на рис. 27.4). Таких фокусів у лінзи безліч, і всі вони розташовані в одній площині — у фокальній площині лінзи, яка проходить через головний фокус лінзи перпендикулярно до її головної оптичної осі.

Які фізичні величини характеризують лінзу?

Фокусна відстань F лінзи — відстань від оптичного центра лінзи до її головного фокуса*.

Одиниця фокусної відстані лінзи в СІ — метр: [ F]  =1 м (m).

Фокусну відстань збиральної лінзи вважають  додатною, а розсіювальної лінзи — від’ємною.

Чим сильніше лінза заломлює світло, тим меншою є її фокусна відстань.

Фізичну величину, яка характеризує заломні властивості лінзи та обернена до її фокусної відстані, називають оптичною силою D лінзи:

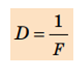
 Одиниця оптичної сили — діоптрія: [ D]  =1 дптр.

1 діоптрія — це оптична сила такої лінзи, фокусна відстань якої дорівнює 1 метру: 1 дптр = 1 м–1.

Якщо лінза збиральна, її оптична сила є додатною, якщо лінза розсіювальна, її оптична сила є від’ємною.

Як побудувати зображення в лінзі?

Будь-який предмет можна подати як сукупність точок. Кожна точка предмета висилає (або відбиває) промені в усіх напрямках. У створенні зображення в лінзі бере участь безліч променів, однак для побудови зображення деякої точки S досить знайти точку перетину будь-яких двох променів, що виходять із точки S і проходять крізь лінзу. Зазвичай для цього обирають два із трьох «зручних променів». Точка S1 буде дійсним зображенням точки S, якщо в точці S1 перетинаються власне заломлені промені . Точка S1 буде уявним зображенням точки S, якщо в точці S1 перетинаються продовження заломлених променів .

Зобразимо схематично предмет стрілкою AB і віддалимо його від збиральної лінзи на відстань, більшу за 2F .

Спочатку побудуємо зображення точки B, для чого скористаємося двома «зручними променями» (промені 1 і 2). Після заломлення в лінзі вони перетнуться в точці B1. Отже, точка B1 є дійсним зображенням точки B. Оскільки предмет AB розташований перпендикулярно до головної оптичної осі l лінзи, його зображення теж буде розташоване перпендикулярно до неї. Тому для побудови зображення точки А проведемо перпендикуляр із точки B1 на головну оптичну вісь l. Точка A1 перетину перпендикуляра й осі l і є зображенням точки А. Отже, A B1 1 — зображення предмета AB, одержане за допомогою збиральної лінзи. Бачимо: якщо предмет розташований за подвійним фокусом збиральної лінзи, його зображення, одержане за допомогою лінзи, є дійсним, зменшеним, перевернутим. Таке зображення виходить, наприклад, на сітківці ока або на матриці фотоапарата.

Із ... бачимо: зображення предмета AB, одержаного за допомогою збиральної лінзи у випадку, коли предмет розташований між фокусом і лінзою, є уявним, збільшеним, прямим.

Таким чином, розміри та вид зображення, одержаного за допомогою збиральної лінзи, залежать від відстані між предметом і лінзою.

Побудова зображень, одержаних за допомогою розсіювальної лінзи, показує, що розсіювальна лінза завжди дає уявне, зменшене, пряме зображення предмета .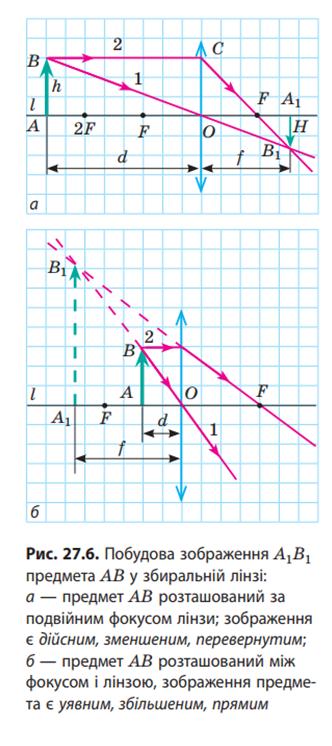

 Часто буває, що предмет більший за лінзу або частина лінзи закрита непрозорим екраном (наприклад, лінза об’єктива фотоапарата). На ... видно, що промені 2 і 3 не проходять крізь лінзу, але їх, як і раніше, можна використати для побудови зображення. Оскільки реальні промені, що вийшли з точки B, після заломлення в лінзі перетинаються в одній точці — B1 , то «зручні промені», за допомогою яких будується зображення, теж перетиналися б у точці B1 .

Формула тонкої лінзи. Лінійне збільшення лінзи

Визначимо математичну залежність між відстанню d від предмета до лінзи, відстанню f від зображення предмета до лінзи і фокусною відстанню F лінзи. Для цього скористаємося .

Прямокутні трикутники FOC і FA1B1 подібні, тому OC/ A1 B1= FO/ FA1 = . Оскільки OC=h, A1B1 =H, FO=F, FA1 =f – F, отримуємо:

h/ H= F/ f -F . (1)

Прямокутні трикутники BAO і B1A1O подібні, отже, AB/ A1 B1= AO /A1O  , або

h/ H =d/ f  . (2)

Прирівнявши праві частини рівностей (1) і (2), маємо: F/ f -F= d /f ; Ff = df -dF; df = Ff+ dF. Поділивши останню рівність на dfF, отримаємо формулу тонкої лінзи:

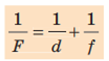
Відношення лінійного розміру H зображення предмета до розміру h самого предмета називають лінійним збільшенням Г лінзи:
 

Відношення лінійного розміру H зображення предмета до розміру h самого предмета називають лінійним збільшенням Г лінзи:

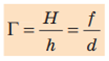
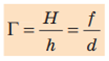
Використані  джерела: Фізика (рівень стандарту, за навчальною програмою авторського колективу під керівництвом Локтєва В. М.) : підруч. для 11 кл. закл. загал. серед. освіти / [Бар’яхтар В. Г., Довгий С. О., Божинова Ф. Я., Кірюхіна О. О.] ; за ред. Бар’яхтара В. Г., Довгого С. О. — Харків : Вид-во «Ранок», 2019. — С.155-160