У чому причина заломлення світла?

Якщо пучок світла падає на межу поділу двох прозорих середовищ, то частина світлової енергії повертається в перше середовище, утворюючи відбитий пучок світла, а частина — проходить через межу в друге середовище, утворюючи пучок світла, який, як правило, змінює напрямок .

Зміну напрямку поширення світла в разі його проходження через межу поділу двох сере довищ називають заломленням світла.      

Промінь, що задає напрямок заломленого пучка світла, називають заломленим променем.

Кут, утворений заломленим променем і перпендикуляром до межі поділу двох середовищ, проведеним із точки падіння променя, називають кутом заломлення.

Кількісний закон, що описує заломлення світла, був установлений експериментально в 1621 р. голландським природознавцем Віллебрордом Снелліусом (1580–1626) й отримав назву закон Снелліуса. Одержимо цей закон за допомогою принципу Гюйґенса.

 Встановлення закону заломлення світла на основі принципу Гюйґенса

Розглянемо плоску хвилю, що падає на межу поділу MN двох середовищ . Напрямок поширення хвилі задамо променями A1A і B1B, паралельними один одному та перпендикулярними до хвильової поверхні AC.

 Зрозуміло, що спочатку поверхні MN досягне промінь А1А, а вже після цього її досягне промінь В1В — через час ∆t =CB/ v1 , де v1 — швидкість світла у першому середовищі.

У момент, коли вторинна хвиля в точці В тільки починає збуджуватися, хвиля від точки А вже пошириться у другому середовищі на відстань AD = v2∆t , де v2 — швидкість світла у другому середовищі. Провівши площину DB, дотичну до всіх вторинних хвиль, одержимо хвильову поверхню заломленої хвилі.

Розглянемо прямокутні трикутники ACB і ADB. У трикутнику ACB кут CAB дорівнює куту падіння α (як кути з відповідно перпендикулярними сторонами), отже, CB = ABsinα. Урахувавши, що CB =v1∆t , знайдемо AB: AB=v1/sinα ∆t (1). Аналогічно в трикутнику ADB кут ABD дорівнює куту заломлення γ , отже, AD =ABsinγ . Урахувавши, що AD = v2∆t , знайдемо AB: AB=v2/sinγ *∆ t(2). Прирівнявши праві частини рівностей (1) і (2), маємо: sin a /sin γ =v1/v2= n21, де n21 — відносний показник заломлення (показник заломлення середовища 2 відносно середовища 1) — незмінна для двох даних середовищ величина, яка не залежить від кута падіння світла.

Закони заломлення світла (закони Снелліуса)

1. Промінь падаючий, промінь заломлений і перпендикуляр до межі поділу двох середовищ, проведений із точки падіння променя, лежать в одній площині.

2. Для двох даних середовищ відношення синуса кута падіння a до синуса кута заломлення g є величиною незмінною:

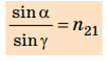
Що характеризує показник заломлення

Відносний показник заломлення показує, у  скільки разів швидкість поширення світла в середовищі 1 більша (або менша), ніж швидкість поширення світла в середовищі 2:

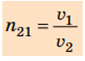
 Саме зміна швидкості поширення світла в разі його переходу з одного прозорого середовища в інше є причиною заломлення світла.

Прийнято говорити про оптичну густину середовища: чим більшою є оптична густина середовища, тим меншою є швидкість поширення світла в цьому середовищі. Так, оптична густина води менша від оптичної густини алмазу, відповідно швидкість світла у воді більша, ніж в алмазі. Зазвичай швидкість світла в середовищі порівнюють з його швидкістю у вакуумі.

Фізичну величину, яка характеризує оптичну густину середовища і показує, у скільки разів швидкість поширення світла в середовищі менша, ніж у вакуумі, називають абсолютним показником заломлення середовища:

 Абсолютний показник заломлення залежить від фізичного стану середовища (температури, густини та ін.) і від частоти світлової хвилі. Тому в таблицях зазвичай указують або стан середовища і частоту світлової хвилі, або середній показник заломлення для даного діапазону довжин хвиль.

 

Використані джерела: Фізика (рівень стандарту, за навчальною програмою авторського колективу під керівництвом Локтєва В. М.) : підруч. для 11 кл. закл. загал. серед. освіти / [Бар’яхтар В. Г., Довгий С. О., Божинова Ф. Я., Кірюхіна О. О.] ; за ред. Бар’яхтара В. Г., Довгого С. О. — Харків : Вид-во «Ранок», 2019. — С. 149-153